vb_app

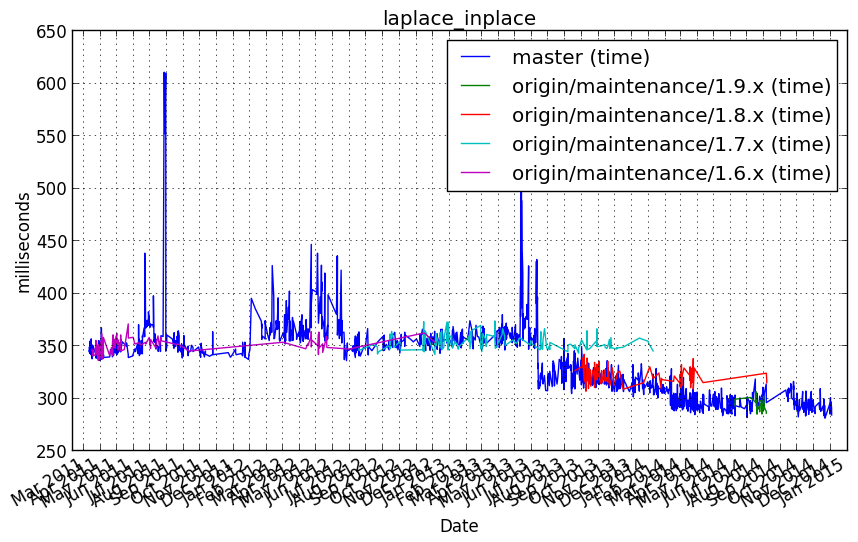
laplace_inplace

Benchmark setup

import numpy as np
N = 150
Niter = 1000
dx = 0.1
dy = 0.1
dx2 = dx*dx
dy2 = dy*dy

def num_update(u, dx2, dy2):
    u[1:-1,1:-1] = ((u[2:,1:-1]+u[:-2,1:-1])*dy2 +
                    (u[1:-1,2:] + u[1:-1,:-2])*dx2) / (2*(dx2+dy2))

def num_inplace(u, dx2, dy2):
    tmp = u[:-2,1:-1].copy()
    np.add(tmp, u[2:,1:-1], out=tmp)
    np.multiply(tmp, dy2, out=tmp)
    tmp2 = u[1:-1,2:].copy()
    np.add(tmp2, u[1:-1,:-2], out=tmp2)
    np.multiply(tmp2, dx2, out=tmp2)
    np.add(tmp, tmp2, out=tmp)
    np.multiply(tmp, 1./(2.*(dx2+dy2)), out=u[1:-1,1:-1])

def laplace(N, Niter=100, func=num_update, args=()):
    u = np.zeros([N, N], order='C')
    u[0] = 1
    for i in range(Niter):
        func(u,*args)
    return u

Benchmark statement

laplace(N, Niter, func=num_inplace, args=(dx2, dy2))

Performance graph

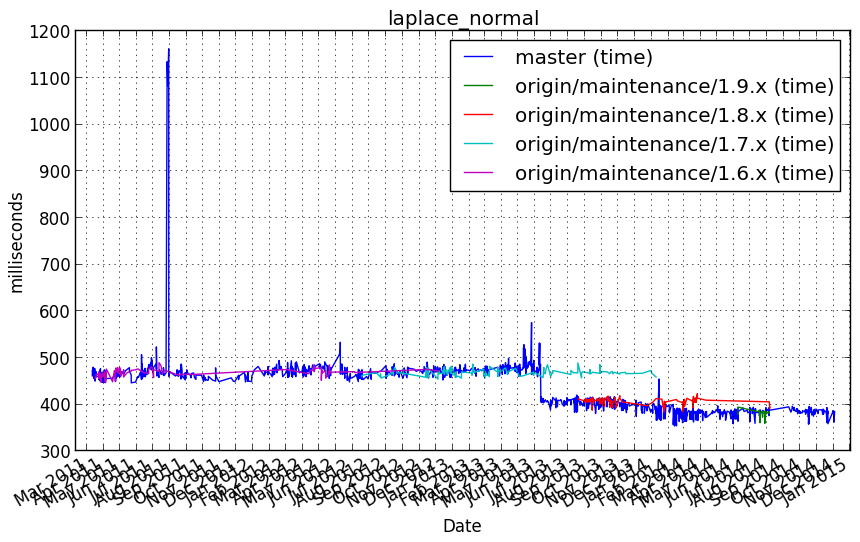
laplace_normal

Benchmark setup

import numpy as np
N = 150
Niter = 1000
dx = 0.1
dy = 0.1
dx2 = dx*dx
dy2 = dy*dy

def num_update(u, dx2, dy2):
    u[1:-1,1:-1] = ((u[2:,1:-1]+u[:-2,1:-1])*dy2 +
                    (u[1:-1,2:] + u[1:-1,:-2])*dx2) / (2*(dx2+dy2))

def num_inplace(u, dx2, dy2):
    tmp = u[:-2,1:-1].copy()
    np.add(tmp, u[2:,1:-1], out=tmp)
    np.multiply(tmp, dy2, out=tmp)
    tmp2 = u[1:-1,2:].copy()
    np.add(tmp2, u[1:-1,:-2], out=tmp2)
    np.multiply(tmp2, dx2, out=tmp2)
    np.add(tmp, tmp2, out=tmp)
    np.multiply(tmp, 1./(2.*(dx2+dy2)), out=u[1:-1,1:-1])

def laplace(N, Niter=100, func=num_update, args=()):
    u = np.zeros([N, N], order='C')
    u[0] = 1
    for i in range(Niter):
        func(u,*args)
    return u

Benchmark statement

laplace(N, Niter, func=num_update, args=(dx2, dy2))

Performance graph

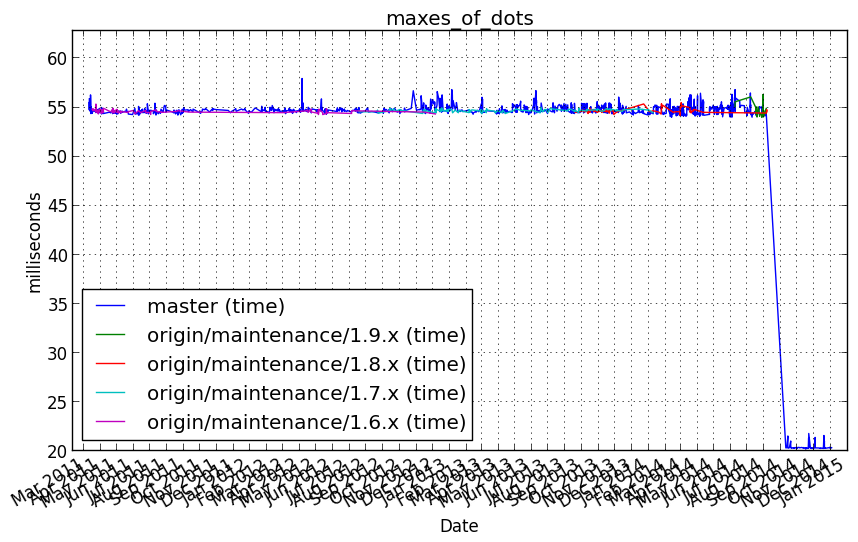
maxes_of_dots

Benchmark setup

import numpy as np
np.random.seed(1)

nsubj = 5
nfeat = 100
ntime = 200

arrays = [np.random.normal(size=(ntime, nfeat)) for i in xrange(nsubj)]

def maxes_of_dots(arrays):
    """
    A magical feature score for each feature in each dataset
    :ref:`Haxby et al., Neuron (2011) <HGC+11>`.
    If arrays are column-wise zscore-d before computation it
    results in characterizing each column in each array with
    sum of maximal correlations of that column with columns
    in other arrays.

    Arrays must agree only on the first dimension.

    For numpy it a join benchmark of dot products and max()
    on a set of arrays.
    """
    feature_scores = [ 0 ] * len(arrays)
    for i, sd in enumerate(arrays):
        for j, sd2 in enumerate(arrays[i+1:]):
            corr_temp = np.dot(sd.T, sd2)
            feature_scores[i] += np.max(corr_temp, axis = 1)
            feature_scores[j+i+1] += np.max(corr_temp, axis = 0)
    return feature_scores

Benchmark statement

maxes_of_dots(arrays)

Performance graph